王雪松，徐振洋*，李小帥，張金銘
（遼寧科技大學 礦業工程學院，遼寧 鞍山 114051）
摘 要：為解決露天礦山配礦出礦點位置爆堆品位分布不均勻的問題，按照出礦位置對應生產能力與鏟裝設備，確定最小配礦單元大小，將爆堆離散化形成獨立的配礦單元，使離散化的配礦單元作用于鏟運與配礦工作，通過距離冪反比法估值對離散單元中礦石各組分的品位進行估值，采用PSO算法確定距離反比法中的最優冪次，將不同計算方法下的品位值與實測結果進行對比，優化距離冪反比法估值爆堆品位方法的準確性，減少配礦單元中品位估算的誤差對配礦結果的影響。
關鍵詞：配礦優化；PSO算法；配礦單元；距離反比法
OPTIMIZATION OF OPEN PIT MINE BLASTING REACTOR UNIT DIVISION METHOD AND DETERMINATION OF ORE OUTPUT GRADE
Wang Xuesong1，Xu Zhenyang1，Li Xiaoshuai1*，Zhang Jingming
(School of Mining Engineering, University of Science and Technology Liaoning, Liaoning, Anshan, 114051，China )
Abstract：In order to solve the problem of uneven distribution of blasting heap grade at the ore distribution point of open pit mine, the minimum size of ore distribution unit is determined according to the corresponding production capacity and shovel loading equipment at the ore distribution location, and the blasting heap is discretized to form an independent ore distribution unit, so that the discrete ore distribution unit acts on the shovel and ore distribution work and is inversely proportional to the power of distance. The PSO algorithm is used to determine the optimal power of the inverse distance ratio method. The grade values under different calculation methods are compared with the measured results. The accuracy of the inverse distance ratio method is optimized to reduce the error pair of grade estimation in the ore blending unit. Influence of ore matching results.
Key words：ore distribution optimization, PSO algorithm, ore distribution unit, inverse distance ratio method
0 引言
目前礦業形勢下，粗放式管理顯然無法滿足礦山工作要求，由粗放式向精細化管理的轉變成為礦業發展的新趨勢[1]，在露天鐵礦山的日常生產工作中，采場礦石質量控制作為一項重要工作深受礦山企業的重視，而實施配礦工作離不開爆堆的礦石質量情況等基礎信息[2].露天采場因出礦點數量眾多、品位分布不均勻，這就為日常配礦工作造成了很大影響，從采場出礦點源頭產生的問題直接導致了配礦效率低下、配礦方案可行性差等問題。
因此，從采場出礦點的源頭處，研究優化露天礦山爆堆配礦單元的劃分與其出礦品位的確定方法應當趨于精細化，配礦單元的劃分工作主要分為確定配礦單元大小、推進方式及出礦品位確定幾個方面。其中距離冪次反比法廣泛應用于出礦品位的確定中，但此方法中冪次的確定受到了廣泛的關注，基于此，通過PSO算法對距離冪次反比法中的冪次進行計算，PSO算法的簡單易行、收斂速度快、優化效率高等優勢，處理非線性問題中得到很好的效果[3]，在確定冪次的過程中，設定目標函數，給出算法中所需的各項參數，使結果收斂于最優解，將此方法所得的冪次作用于距離冪次反比法之中，將得到的品位值與實測值及平均系數法計算值進行比較。
1 配礦單元的劃分
1.1 確定配礦單元大小
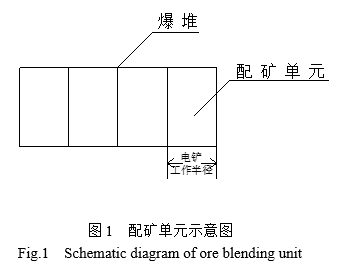
采用平均品位表示整個爆區的品位情況，顯然無法真實的反應供礦品位，因此，需要將整個爆區劃分為若干個配礦單元，配礦單元的劃分中涉及配礦單元礦量、相鄰單元步距、爆堆推進方式幾個方面，露天鐵礦山采區具有多個出礦位置，每個出礦位置含有供電鏟工作至少2-3天的礦量[4]。
劃分配礦單元的時，國內的很多研究按照炮孔數量劃分，以每個單元內存在3-4個或7-8個炮孔為規則，區域內含有多個品位控制點[5]。區域劃分時對鏟裝設備、推進方式、生產能力等方面考慮不足。因此，確定配礦單元大小、計算出礦點品位、劃分爆堆的推進方式需要按照一定的規則進行。
露天礦山日開采計劃各出礦點需要滿足品位穩定、礦石質量均衡等條件，因此，在編制日開采計劃時需要將各出礦點爆堆劃分為合適大小的配礦單元，避免礦石暴露時間過長導致的礦石質量降低，增加鏟裝效率，減少不必要的損失。
配礦步距確定以鏟裝位置爆堆為起始點，采用固定大小的矩形劃分配礦單元，相鄰配礦單元之間的步距為電鏟工作半徑。
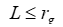
(1)
式中，L為配礦單元步距；rg為電鏟工作半徑。
隨著礦山機械化的發展，礦山設備趨于大型化，電鏟在工作過程中一般移動較少，以此減少不必要的花費，每個出礦點只有一個電鏟進行工作，為生產效率，電鏟日工作量一般為其生產能力的80%以上，考慮到出礦點各處地形等原因，以電鏟電鏟生產能力確定配礦單元大小的范圍，出礦位置的劃分方式根據出礦臺階所謂對應電鏟生產能力的60%，且不大于電鏟的最大日生產能力，即：
一個出礦點的爆堆按照所確定的大小關系，平均劃分。
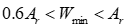
(2)
式中，Ar為對應電鏟的最大生產能力；Wmin為最小配礦單元所含礦量。
配礦單元劃分大小確定后，將可出礦的爆堆按照大小規則劃分，這樣的劃分方式便于統計出礦點礦量，此處電鏟生產能力所編制計劃時間的長短有所不同，這樣的方法有利于生產計劃的編制，便于礦山企業在生產中進行管理。
1.2 配礦單元開采順序
露天礦推進方式指根據臺階主推進方向及設備能作業方向可能的采掘方式，采場提供的臺階主推進方向以及自由面，根據適用電鏟效率的采掘寬度和電鏟日生產能力，產生出多種可能的推進方式[6]。按照采場推進方式將劃分后的出礦點排序，從臺階自由面的最右側起，按照次序排列，優先開采起始的下一排配礦礦單元，即采用電鏟移動距離最小的順序方式排序配礦單元，如圖3所示。
此種開采方式可減少電鏟頻繁移動的次數，也使得礦山進行生產計劃編制時進行配礦單元的選擇。
1.3 出礦品位的確定
礦石出礦品位是配礦工作的基礎參數，國內大部分礦山采用平均系數法完成出礦點品位的預測，此方法便于操作計算量小，但具有局限性，有時無法準確的估算出礦石的品位。在地質學領域中，許多具有空間相關性的變量一般采用距離冪次反比估值法進行[7]。相比平均系數法，距離冪次反比法引入預估點品位的影響與距離相關，距離越近影響越大，反之影響較小[8]。針對距離冪次反比法，從不同的層次和角度提出相應的解決途徑，主要在于確定最優參估樣品數據是此方法在實際應用中必須要考慮的問題[9]。
兩種品位估值方法廣泛應用，具有較好的品位預測能力，相比于露天礦山出礦點的實際測量值，兩種方法均存在誤差，對比不同方法下計算結果誤差，介紹不同計算方法的區別，對比不同方法下計算結果的誤差。
距離冪次反比方法的基本流程如下：
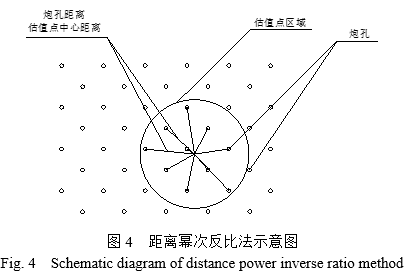
以觀測點的中心為原點，最小配礦單元的范圍大小相同的區域作為估值區域，連接每個探測孔與觀測點中心確定距離，采用距離冪反比公式計算估值區域品位。
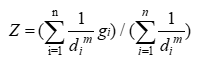
(3)
式中，Z為配礦單元中心點的品位；di為配礦單元中第i個炮孔的距中心點的距離；gi為第i個炮孔的礦石品位；m為冪指數。
2 基于PSO算法確定最優冪次
粒子群優化算法的基本思想是通過群體中個體之間的協作和信息共享來尋找最優解，PSO的優勢在于簡單容易實現并且沒有很多的參數調節，在距離冪次反比法中的冪次確定中，各控制點距離中心的位置對中心點的品位值影響并不相同，隨著距離的增大呈現近似正相關，在冪次計算時制約計算結果的除各控制點的品位值以外，還有所處位置的距離，故利用PSO算法進行求解非常適合最優冪次的求解中。
2.1 PSO算法
粒子群算法[10]，也稱作粒子群優化算法或鳥群覓食算法，是基于鳥群覓食行為而提出的，開發的一種新的進化算法，其特點是從隨機解出發，通過迭代尋找最優解，達到運算目的。PSO算法具有參數少、實現容易、收斂速度快、便于理解等優點，算法高效適合運用于尋找品位計算中最優冪次的計算中[11]。
PSO的運算原理是初始化一群隨機粒子，從初始解開始尋找最優解，運算中，通過兩種方法更新粒子，第一種方法是由粒子本身所找到的最優解，此解成為個體極值，另一個方法是整個種群目前找到的最優解，也就是全局極值9999。
假設存在一個D維的目標搜索空間，與一個由N個粒子組成的群落，其中第i個粒子表示為一個D維的向量，即：
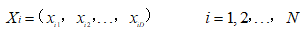
(4)
粒子的速度也為一個D維的向量，表示位置的改變，即：
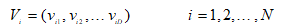
(5)
粒子個體的最優極值記為p
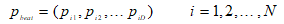
(6)
整個粒子群搜索到最優位置稱為全局極值記為p，即：
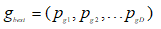
(7)
兩個最優位置找到后，粒子的速度和位置更新通過以下公式進行，即：
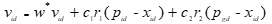
(8)
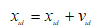
(9)
式中，w為慣性系數；c1與c2為加速系數也被稱為學習因子；r1與r2是區間為[0,1]服從均勻分布的兩個獨立隨機數。
2.2 應用實例
本試驗共選取了8個取值塊段，包括塊段中各控制點的品位與其距離中心點的距離。其中1號塊段的基礎信息如表1所示。
表1 1號塊段品位表
Table 1 1 block grade table
針對距離冪次反比中的冪次確定問題，采用PSO算法，并進行對比，實驗共進行1000次迭代計算。其參數設置如表2所示：
表2 算法參數設置表
Table 2 algorithm parameter setting table
在本問題中，粒子的適應值函數可定義為預估點與實測點的差值平方，滿足該函數值最小時，即為函數的最優解，進而得到最優冪次。即：
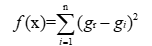
(10)
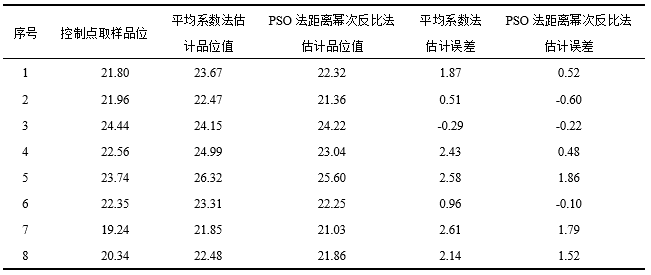
2.3 結果分析式中：
為點位實測品位，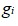
為控制點i的品位估計值。
根據3種結果的對比結果如表3所示，對比表中的數據可發現由PSO方法計算冪次反比誤差方法明顯優于平均系數法，并且結果趨向于控制點的取樣品位。
表3 計算結果表
Table 3 calculation results table
通過誤差圖像進行分析發現，相比平均系數法估計品位值，8組數據中PSO法所計算的距離冪次法均更接近控制點取樣的品位值實際數據，但個別點位的誤差仍然較大。總的來說，PSO算法計算得出的冪次具有良好的預測性，此方法適用于該數值的確認，提升出礦品位值的計算精度。
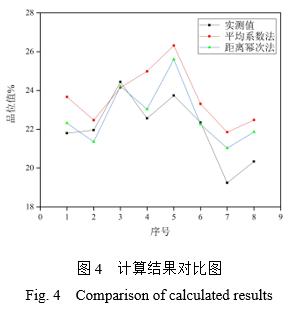
（1）進行配礦單元劃分，以電鏟工作半徑確定配礦單元步距，確定配礦單元的最小礦量為電鏟生產能力的60%，得出以“蛇形”方式推進的開采順序。3 結 論
（2）根據出礦點品位計算的特征，使用距離冪次反比法確定品位值，使用PSO算法設置各項參數，得到了以偏差最小的目標函數。
（3）以PSO算法得出的品位值相較于平均系數法得出的品位值更接近塊段實測品位值。
[1] 王李管,宋華強,畢林,等.基于目標規劃的露天礦多元素配礦優化[J].東北大學學報(自然科學版),2017,38(07):1031-1036.
[2] 井石滾,盧才武,顧清華.基于GIS的露天礦生產配礦數字化管理系統[C].國際遙感大會.杭州:[S.N.],2010: 426-429.
[3] 陳前宇,陳維榮,戴朝華,等.基于改進PSO算法的電力系統無功優化[J].電力系統及其自動化學報,2014,26(02):8-13.
[4] 李章林,王平,張夏林.距離冪次反比法的改進與應用[J].金屬礦山,2008,V38(04):88-92.
[5] 陳彥亭,鞏瑞杰,南世卿,等.露天礦智能配礦系統研發與應用[J].現代礦業,2016(04):206-210.
[6] 崔方寧,邵明國,趙然磊,等.基于三維可視化建模技術的礦量計算方法[J].現代礦業,2014(08):61-63.
[7] 王仁鐸,胡光道.線性地質統計學[M].北京:地質出版社,1988.
[8] Shepard D.A two-dimensional interpolation function for irregularly-spaced data[C].Proc Acm National Conference.1968.
[9] Watson D F.A refinement of inverse distance weighted interpolation[J].Geo-Processing,1985,2(02):315-327.
[10] J.Kennedy,R.Eberha.Particles warm optimization[C].Neural Networks,1995.Proceedings.,IEEE International Conference on.IEEE,1995:1942-1948.
[11] 朱永紅,丁恩杰,胡延軍.PSO優化的能耗均衡WSNs路由算法[J].儀器儀表學報,2015,36(01):78-86.