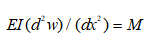劉舒朗¹，陳慶凱¹，谷  明²，溫海波¹，郭趙杰¹

（1 東北大學資源與土木工程學院，遼寧 沈陽  110819；2 南芬露天鐵礦，遼寧 本溪  117014)

摘  要：在露天臺階爆破中，各爆破參數之間相互關聯，共同影響著爆破效果。為了分析爆破參數對露天臺階爆破效果的影響，國外有學者引入材料力學中懸臂梁的理論對炮孔負擔崩落的巖石進行分析，將抗彎剛度引用到了露天臺階爆破中，但國內對此鮮有研究。通過對巖梁模型的分析和計算，推導出了露天臺階爆破中抗彎剛度值的計算公式。在抗彎剛度值計算公式中，剛度比例系數至關重要，直接影響露天臺階爆破時的炸藥能量分布的均勻性，文獻中的數值模擬結果驗證了這種影響。針對南芬露天鐵礦臺階爆破參數，從剛度角度分析了采用310 mm孔徑的炸藥單耗比250 mm孔徑的炸藥單耗高的原因。分析表明剛度比例系數越大，抗彎剛度值越小，巖體所受阻力越小，炸藥在巖體中分布地越均勻，臺階變形越大，巖體破碎越容易，并且可以有效地降低炸藥單耗。

關鍵詞：臺階爆破；爆破參數；抗彎剛度值；剛度比例系數；巖梁模型；炸藥單耗

ANALYSIS OF INFLUENCE OF STIFFNESS RATIO ON OPEN-PIT BENCH BLASTING

Liu Shulang¹，Chen Qingkai¹，Gu Ming²，Wen Haibo¹，Guo Zhaojie¹

(1. School of Resources and Civil Engineering, Northeastern University, Shenyang 110819，China;

 2. Nanfen Open Pit Mine, Benxi 117014，China)

Abstract: In the open-pit bench blasting, the blasting parameters are related to each other, which affects the blasting effect. In order to analyze the influence of blasting parameters on the effect of open-pit bench blasting, some foreign scholars have introduced the theory of cantilever beam in the mechanics of materials to analyze the rock that bench blasting needs to break, and cited bending stiffness in open-air bench blasting, however, few domestic studies about it at home. Through the analysis and calculation of the rock beam model, the applicable relation of the bending stiffness values is deduced. In the calculation formula of the bending stiffness values, the stiffness ratio is very important, which directly affects the uniformity of the explosive energy distribution in the open bench blasting. The numerical simulation results in the literature verify this result. According to the parameters of bench blasting in Nanfen open-pit iron mine, the reason why the powder factor of explosive with 310mm hole diameter is higher than that with 250mmhole diameter is analyzed from the perspective of stiffness. It is proved that the larger the stiffness ratio, the smaller the value of the bending stiffness, the lower the resistance of the rock mass, the more uniform the explosive is distributed in the rock mass, the greater the bench deformation, the easier the rock fragmentation, and can effectively reduce the powder factor.

Key words: bench blasting, blasting parameters, bending stiffness value, stiffness ratio, rock beam model, powder factor

0  引  言

在露天臺階爆破中，孔網參數、臺階高度和炸藥單耗是影響爆破效果的三個重要因素，并且相互之間有著一定的比例關系^[1]，如果這些參數選取不合理，爆破效果會變差，嚴重時甚至會影響礦山的正常生產。因此，如何合理的選取爆破參數一直是學者們研究的熱點^[2]。隨著科研水平的提高，各學科之間產生了很多交叉應用。通過結合材料力學中梁的相關理論，學者們將各類梁的模型引入到了巖石開挖過程和采場圍巖穩定性分析中，取得了一定的成就。不過在國內，梁的理論主要被應用于地下采場的頂板巖層分析，巖梁模型^[3]就是基于梁的理論而提出的一種力學模型，文獻^[4-7]均將頂板巖層的巖板模型簡化為巖梁模型進行分析，取得了一定的效果。而在國外，Ash^[8]和Smith^[9]將梁的理論應用在露天臺階爆破中，將單個炮孔負擔崩落的巖石簡化為以懸臂梁為基礎的巖梁模型，通過對其進行分析提出了剛度比例系數的概念。研究發現：調整抵抗線和臺階高度，使剛度比例系數的值在2-3之間，可起到使礦巖破碎更加均勻、降低炸藥單耗等作用。

1  剛度比例系數的由來

1.1 抗彎剛度及抗彎剛度值

在露天臺階爆破中，Ash^[10]認為由炮孔周圍彎曲破裂引起的巖石破碎是由炮孔負擔崩落的巖石的剛性狀態控制的，這種剛性狀態叫做剛度。由于炮孔周圍的巖石破壞被看作是懸臂梁模型的彎曲過程，因此這種剛度也被稱為抗彎剛度。有別于材料力學中的抗彎剛度，這種剛度實質為假設的懸臂梁模型的彈性系數，即懸臂梁梁身部分整體所受應力與應變的比值，其大小用抗彎剛度值K來表示，K值的大小決定了被爆巖石產生單位位移所需外力的大小。K值越大，炸藥爆炸時所受阻力越大，臺階變形程度越低；K值越小，炸藥爆炸時所受阻力越小，臺階變形程度越高。

1.2 抗彎剛度值K的推導

露天臺階爆破中的抗彎剛度值K的推導離不開對巖梁模型的分析。巖梁模型是建立在將炮孔負擔崩落的巖石作為懸臂梁進行分析的基礎上提出的一種假設，將單個炮孔負擔崩落的巖石徑向開裂近似地看作炮孔周圍的若干個巖梁以臺階坡底面作為固定端進行旋轉的過程。如果幾個炮孔一起起爆，或在極短間隔時間內連續起爆，將使它們負擔崩落的巖石或多或少作為一個整體，也就是說組合巖體將像寬梁或板一樣發揮作用。

在推導抗彎剛度值的公式時，對巖梁模型做如下假設：

（1）巖梁為下端固定垂直放置的懸臂梁。

（2）認為其變形很小。

（3）巖梁的橫截面為矩形截面。

（4）巖梁模型受力均勻。

（5）臺階坡面角為90°。

（6）不設置超深和填塞。

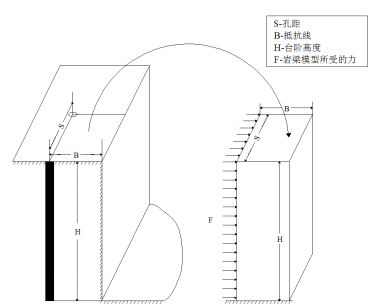
圖1  露天臺階爆破中巖梁模型受力示意圖

Fig.1  Schematic diagram of rock beam model in the open-pit bench blasting

在露天臺階爆破中，單個炮孔周圍的巖梁模型（懸臂梁）及其受力情況如圖1所示。在圖1中，懸臂梁的高度（臺階高度）為H、寬度（孔距）為S、厚度（抵抗線）為B。在計算上，抗彎剛度的實質為巖梁模型中懸臂梁的彈性系數，也就是巖梁模型里懸臂梁所受的應力與產生的應變的比值，故其表達式可以通過材料力學^[11]中的公式推導得到。首先計算懸臂梁因為受力而引起的彎曲變形量，即撓度：

撓曲線近似微分方程：